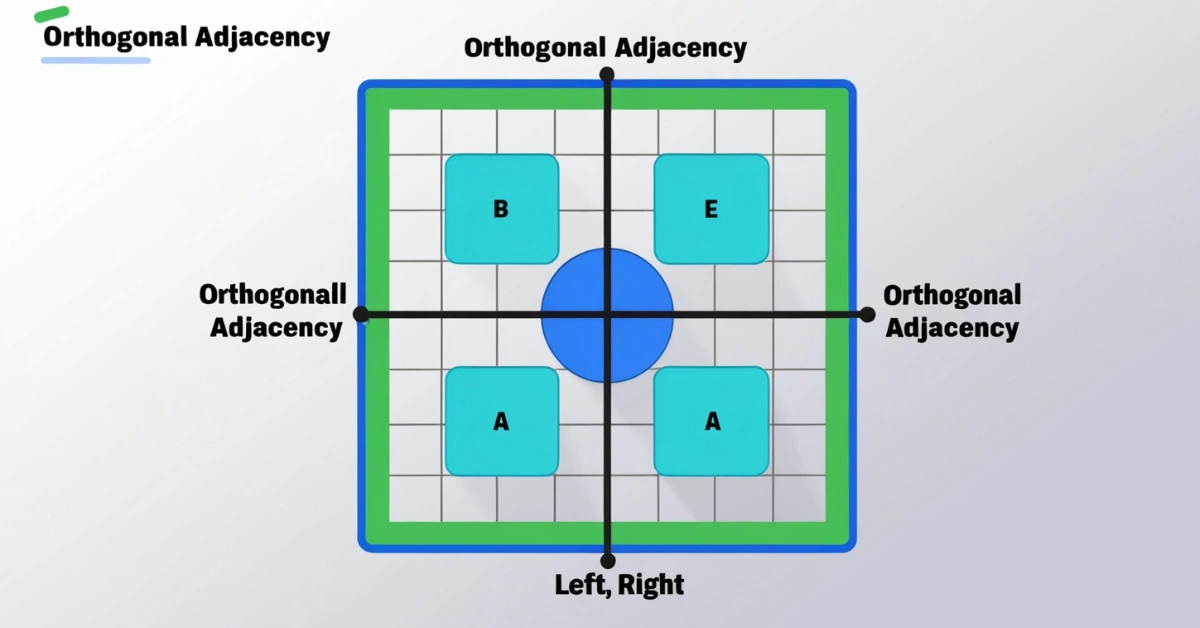
In the world of computers, math and games, one term that often comes up is “Orthogonally Adjacent.” You might hear it when solving puzzles, writing code for a maze or learning geometry. But what does it really mean? And why is it important?
What Does Orthogonally Adjacent Mean?
The word “orthogonal” might sound complicated, but it’s easy to understand. The term ‘orthogonal’ is rooted in Greek, combining words that relate to ‘right’ and ‘angle,’ which together describe something positioned at a 90-degree angle.
In a grid such as a chessboard, spreadsheet, or pixel layout each square is referred to as a cell. When two cells are described as orthogonally adjacent, it means they are positioned next to each other either horizontally or vertically, but not diagonally.
For example, in a 2D grid:
- The cell to the left, right, above, or below a center cell is orthogonally adjacent.
- The cells touching the corners (diagonals) are not considered orthogonally adjacent.
Why Orthogonal Movement Is Preferred in Many Algorithms?
Orthogonal movement (4 directions) has several computational advantages over 8-way movement:
- Fewer conditions to check
- More predictable performance
- Reduced branching in decision trees
Algorithms like A, BFS, and DFS often perform better when limited to 4-directional checks especially when obstacles are placed in a structured grid.
Movement Options in Grid Based Systems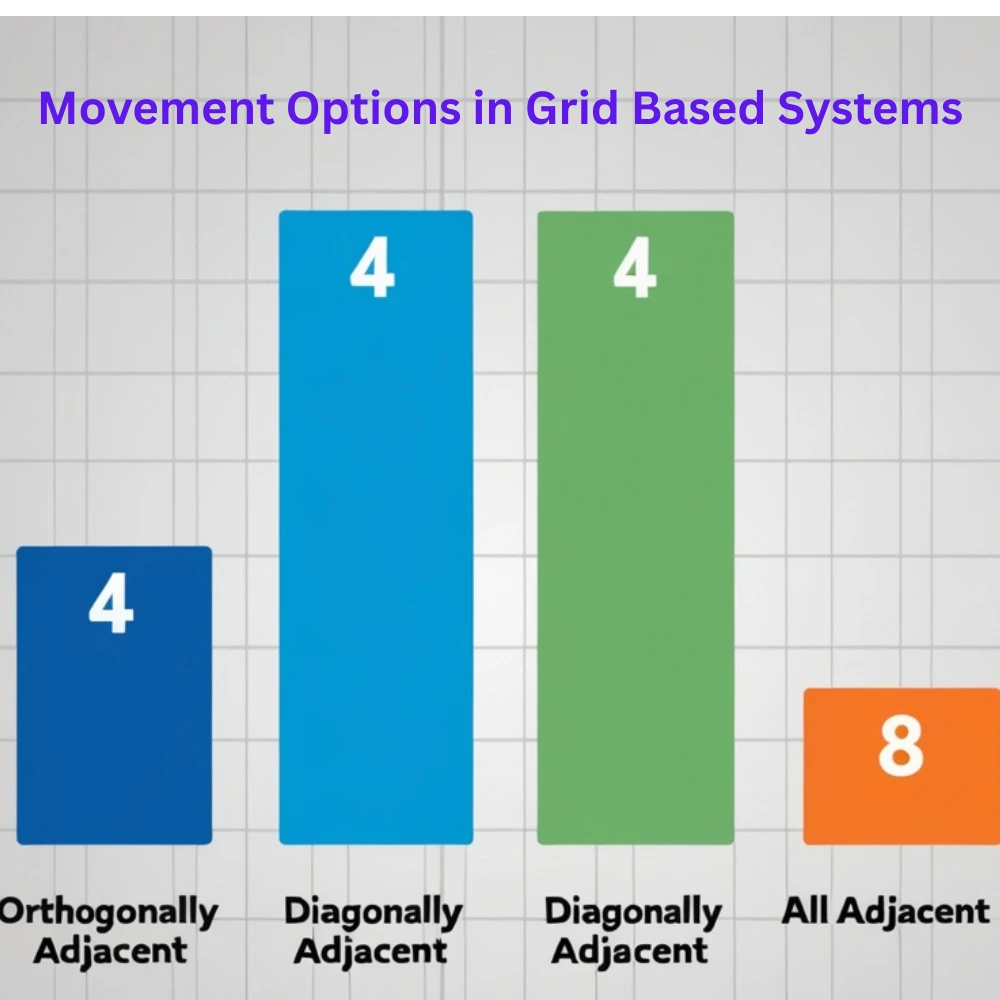
In grid based systems, such as video games, pathfinding algorithms, robotics, and image processing movement options define how a unit, player, or program can travel from one cell to another. These systems are often structured as 2D grids, and the movement rules impact how efficiently and logically a task is completed.
Visual Example of Orthogonal Adjacency
Imagine this 3×3 grid:
[ ] [X] [ ]
[X] [C] [X]
[ ] [X] [ ]
In this grid:
- “C” is the center cell.
- The “X” cells are orthogonally adjacent to “C.”
- The corner cells (not marked) are not orthogonally adjacent.
This kind of layout is often seen in mazes, board games, tile based games and more.
Where Are Orthogonally Adjacent Cells Used?
Orthogonally adjacent cells are used in many fields. Here are some of the most frequent ways this concept is applied.
1. Pathfinding Algorithms
When mazes are built or maps are designed for robots, movement from one cell to another is often required. However, in many cases, diagonal movement is not allowed. This means the robot or player can only move in the four main directions: up, down, left, or right.
Some famous algorithms that use orthogonal adjacency include:
- Breadth-First Search (BFS)
- Depth-First Search (DFS)
- A (A-Star)
These algorithms are used in:
- Maze solvers
- Game AI
- GPS and navigation apps
2. Image Processing
In digital image processing, a photo is made up of thousands (or millions) of square shaped pixels. Sometimes, it is necessary to check how pixels are connected. Orthogonal adjacency is used to identify connected regions, such as detecting a shape, a crack, or an object.
For example:
- Detecting a person’s face
- Finding areas of the same color
- Edge detection
In these cases, pixels are treated like cells in a grid, and their neighbors are checked using orthogonal rules.
3. Game Design and Logic Puzzles
Game designers use orthogonal adjacency because it’s:
- Easy for players to understand visually.
- Simple to process logically.
- Fair in turn-based systems.
Games That Rely on Orthogonal Rules:
- Tetris (blocks snap orthogonally)
- Sudoku (in some variants)
- Nonograms and Slitherlink
- 2048 (tiles combine in straight lines)
Using only vertical and horizontal connections prevents confusion and adds challenge through spatial thinking.
4. Robotics and Motion Planning
In robotics, especially for cleaning robots or warehouse robots, the system calculates movements through a grid based map of the space. If diagonal movement isn’t safe or allowed, the robot’s path is calculated using only orthogonally adjacent positions. This helps avoid collisions and keeps movement predictable.
5. Mathematical Concepts and Grid Geometry
In math, grids and graphs often use orthogonal adjacency to define connectivity.
For example:
- An object is connected if each cell touches another by an edge.
- A shape is considered orthogonally convex when each horizontal and vertical line passing through it intersects a continuous stretch of cells.
This helps in topics like:
- Graph theory
- Combinatorics
- Geometry
6. Flood Fill and Coloring Algorithms
In coloring problems (both real and in code) you might want to fill a shape with color. The flood fill algorithm checks all orthogonally adjacent cells and keeps spreading the color. It stops when it hits a wall or a different color. This idea is used in:
- Paint programs (like the “bucket tool”)
- Shape detection
- Terrain generation in games
Orthogonally Adjacent vs Diagonally Adjacent
This comparison makes it easier to grasp the differences.
| Type of Adjacency | Directions Covered |
| Orthogonally Adjacent | Up, Down, Left, Right |
| Diagonally Adjacent | Top-left, Top-right, etc. |
| Full Adjacency (8-way) | All 8 directions |
Knowing which kind of adjacency to use helps in solving problems accurately, especially in code and logic games.
Why It Matters?
So, why do developers, gamers and mathematicians care so much about orthogonally adjacent cells? Because:
- It simplifies calculations.
- It creates clear and consistent rules.
- It avoids ambiguity (unlike diagonal moves that can overlap paths).
- It improves performance in algorithms.
- It mirrors real world limits (like how a robot can’t turn corners instantly).
In short, it provides a clean and structured way to understand how things are connected in 2D environments.
How to Code Orthogonal Adjacency?
In most programming languages, orthogonally adjacent positions in a 2D grid can be represented like this:
# Suppose you’re at cell (x, y)
# These are the four directions (dx, dy)
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
for dx, dy in directions:
new_x = x + dx
new_y = y + dy
# Check if new_x and new_y are within grid boundaries
Final Thoughts
Orthogonally adjacent cells may sound like a small idea, but they are used in big ways across many fields. From helping robots move safely, to solving a puzzle on your phone, this simple concept is the backbone of many digital tools and games.
By understanding this idea, you can become better at designing systems, solving puzzles, and writing smart algorithms. Whether you’re a beginner learning coding or a puzzle lover who wants to improve their skills, mastering orthogonal adjacency is a step in the right direction.